Recurrent Neural Network , 순환신경망
시퀀스 데이터를 처리하는데 특화된 인공신경망으로 ,이전 시점의 정보를 은닉층에 가지고 있다가 다음 출력을 생성한다.
즉 데이터 입력 시 입력데이터와 이전시점의 은닉상태를 모두 사용하여 현재 상태를 계산할 수 있다.
전체코드(강의자료에 있는것을 약간 수정함)
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# Sine 파형 데이터 생성
def create_sine_wave_data(seq_length, num_samples):
X = []
y = []
for _ in range(num_samples):
start = np.random.rand()
x = np.linspace(start, start + 2 * np.pi, seq_length)
X.append(np.sin(x))
y.append(np.sin(x + 0.1))
return np.array(X), np.array(y)
seq_length = 50
num_samples = 1000
X, y = create_sine_wave_data(seq_length, num_samples)
# 데이터셋을 PyTorch 텐서로 변환
X = torch.tensor(X, dtype=torch.float32).unsqueeze(-1)
y = torch.tensor(y, dtype=torch.float32).unsqueeze(-1)
# 모델 정의
class SimpleRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleRNN, self).__init__()
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
h0 = torch.zeros(1, x.size(0), self.hidden_size).to(x.device)
out, _ = self.rnn(x, h0)
out = self.fc(out[:, -1, :]) # 마지막 시간 단계의 출력
return out
input_size = 1
hidden_size = 32
output_size = 1
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = SimpleRNN(input_size, hidden_size, output_size).to(device)
X, y = X.to(device), y.to(device)
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 모델 학습
num_epochs = 100
for epoch in range(num_epochs):
model.train()
outputs = model(X)
optimizer.zero_grad()
loss = criterion(outputs, y.squeeze(-1)) # 출력 차원을 맞춰줌
loss.backward()
optimizer.step()
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')
print('Finished Training')
# 모델 평가
model.eval()
with torch.no_grad():
predicted = model(X).cpu().numpy() # GPU에서 CPU로 변환
# 시각화
plt.figure(figsize=(10, 5))
plt.xlim(0, len(y)) # X축 범위를 데이터 크기에 맞춰 조정
plt.ylim(-1, 1) # Y축 범위를 특정 값으로 제한
plt.plot(y.cpu().numpy().flatten(), label='True') # GPU에서 CPU로 변환 및 flatten
plt.plot(predicted.flatten(), label='Predicted')
plt.legend()
plt.show()
이것은 사인파형을 예측하는 RNN 모델이다.
import와 사인함수 만드는 부분은 생략하고 모델정의부터 보도록 하겠다.

ANN,CNN과 마찬가지로 클래스를 정의하고 상속받고 init함수를 쓰고 있다.
def __init__(self, input_size, hidden_size, output_size):
input_size: 입력데이터의 크기, 이 코드에서는 sine파형의 한 점이므로 1로 설정되어 있다.
hidden_size: 은닉상태의 크기이자 RNN이 시간단계별로 기억하는 정보의 양으로 여기서는 32로 설정했다.
output_size: 최종적으로 예측할 출력값의 크기로, sine파형의 다음에 올 숫자 하나이므로 1로 설정되어 있다.
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
파이토치에서 제공하는 RNN레이어의 기본구조이다.
batch_first=True라는 것은 텐서의 순서를 맞춰주기 위함인데,
파이토치의 입력텐서는 [시퀀스길이, 배치크기, 입력크기] 의 순서를 가진다. 하지만 데이터를 처리할 때는 배치크기가 가장 앞에 오는 것이 직관적이고 쓰기 편해서, 배치크기를 앞으로 보내주는 것이다.
batch_first=True적용 후 입력텐서는 [배치크기, 시퀀스길이, 입력크기] 순서가 된다.
self.fc = nn.Linear(hidden_size, output_size)
ANN때부터 봤던 선형변환으로 은닉상태를 받아서 output크기만큼의 결과를 생성한다. 이 모델의 경우 32개를 받아 1개의 예측을 출력한다.
def forward(self, x):
이제 forward(순전파)함수를 정의하는데,
h0 = torch.zeros(1, x.size(0), self.hidden_size).to(x.device)
초기은닉상태를 만드는 부분
은닉상태는 모델이 학습을 1회이상 진행한 후에 만들어지는 것이므로, 초기에는 은닉상태가 없다. RNN에게 처음에는 아무 정보도 없다는 사실을 알려주는 부분이 바로 이 코드이다.
torch.zeros(..)
모든 요소가 0으로 채워진 텐서를 생성하는 함수이다.
torch.zeros(1, x.size(0), self.hidden_size)
1은 RNN layer의 개수를 의미하는데 여기서는 한 번의 self.rnn만 사용하고 있으므로 layer수=1이다.
x.size(0)는 배치의 크기이다.
x.size()는 텐서의 차원을 반환하는 함수이다.
입력텐서 x 는 [배치크기, 시퀀스길이, 입력크기] 로 되어있다고 위에서 설명했다.
따라서
x.size(0)= 배치크기
x.size(1)= 시퀀스길이
x.size(2)= 입력크기
숫자를 쓰지 않으면 x.size()= [ 배치크기, 시퀀스길이, 입력크기 ] 로 나온다.
self.hidden_size는 은닉상태의 크기, 여기서는 32
.to(x.device)
입력데이터 x가 위치한 장치(GPU or CPU)로 은닉상태를 옮기는 코드
out, _ = self.rnn(x, h0)
self.rnn(x,h0)은 입력데이터와 초기은닉상태를 받아 (out, hidden) 형태로 출력한다.
out은 각 단계에서 출력으로 [배치크기, 시퀀스길이, 은닉상태크기] 형태로 나온다.
hidden은 마지막 단계에서 최종은닉상태로, [레이어 개수, 배치크기, 은닉상태크기] 로 나온다.
이 모델에서는 out 정보만 쓰고 hidden은 쓰지 않고 있다.
시퀀스 전체를 본 뒤 마지막 단계의 출력만 써서 최종예측을 하는 모델이기 때문이다.
만약 다중RNN 레이어를 쓴다면 최종은닉상태를 다음 레이어로 전달해야 하기 때문에 hidden을 써야한다.
참고)
입력 데이터의 차원: [배치 크기, 시퀀스 길이, 입력 크기]
모델에 들어가기 전에 데이터의 기본 차원
RNN 출력의 차원: [배치 크기, 시퀀스 길이, 은닉 상태 크기]
최종 은닉 상태의 차원: [레이어 개수, 배치 크기, 은닉 상태 크기]
레이어 개수가 하나일 때는 [1, 배치 크기, 은닉 상태 크기]로 출력
out = self.fc(out[:, -1, :])
최종적으로 선형모델에 전달해서 예측값을 얻는 코드
out[:, -1, :]
': 콜론' 은 모든 값을 선택한다는 의미
'-1'은 마지막 시간단계의 데이터를 선택한다는 의미
출력차원은 [배치 크기, 시퀀스 길이, 은닉 상태 크기] 로 되어있다.
그러니까 배치크기에 콜론을 써서 모든 배치에 대해 데이터를 선택하고,
시퀀스 길이에는 -1을 써서 시퀀스의 마지막 단계에서 데이터를 선택하고,
은닉상태크기에 콜론을 써서 모든 은닉상태차원을 선택하는것
이 과정에서 시퀀스 길이는 마지막단계만 선택하므로 사라지고, 최종적으로 [배치크기, 은닉상태크기] 가 출력된다.
이것을
self.fc = nn.Linear(hidden_size, output_size) 에 전달하면
선형변환은 배치 크기와 상관없이 각 배치의 데이터에 동일하게 작동하므로,
[은닉상태크기, 출력크기] 형태의 결과를 받아 출력을 생성함 (이 경우에는 output_size=1 이므로 값 1개를 출력함)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
파이토치의 연산을 GPU에서 할건지 CPU에서 할건지 정하는 부분
model = SimpleRNN(input_size, hidden_size, output_size).to(device)
모델을 생성하고, .to(device)로 모델을 위에서 지정한 장치로 이동
X, y = X.to(device), y.to(device)
마찬가지로 x와 y도 지정한 장치로 이동

criterion = nn.MSELoss()
손실함수
ANN에서는 CrossEntropyLoss()를 사용했다. 이는 분류문제에 적합하며, 확률분포를 비교해서 손실을 계산한다.
반면 MSELoss()는 회귀문제에서 자주 사용되는 손실함수로, 예측값과 실제값 간의 차이를 제곱하여 평균을 낸 것이다. 제곱을 하므로 예측과 정답사이 차이가 클 수록 패널티가 강해진다.
참고)회귀문제란?
연속적인 값을 예측하는 문제로 출력이 숫자나 실수로 나타남
예를 들어 주식가격 예측, 날씨 예측 등
회귀문제와 대비되는 개념은 분류문제
분류문제는 클래스나 범주를 예측하는 문제로 이미지 분류, 의료진단 등이 있다.
optimizer = optim.Adam(model.parameters(), lr=0.01)
Adam도 최적화 알고리즘 중 하나이다. 최신 모델이고 적응형 학습률을 사용하며, 데이터가 크거나 신경망이 복잡할 때 잘 작동하는 편이다. 학습속도도 빠른편이다. 반면 이전에 보았던 SGD는 가장 기본적인 경사하강법으로, 고정된 학습률을 사용한다. 간단하고 직관적이지만 학습속도가 느릴 수 있다.

num_epochs = 100
for epoch in range(num_epochs):
100번 반복학습을 한다
참고로
for epoch in range(100):
이런 코드를 써도 기능적으로는 동일하게 동작하지만, 100이라는 숫자를 직접 하드코딩 하는것과 비교하여 원래 코드는 num_epochs를 따로 줘서 직관적으로 알아보기 쉽게 썼다는 차이가 있다.
model.train()
파이토치에서 모델이 학습모드에 있음을 설정하는 함수
참고로 파이토치 모델의 모드는 train() 과 eval() 의 두 가지 모드가 있다.
학습모드에서는 드롭아웃이나 배치정규화등이 일어나고, 평가모드(또는 예측모드)에서는 드롭아웃등을 하지 않는다.
outputs = model(X)
optimizer.zero_grad()
loss = criterion(outputs, y.squeeze(-1))
criterion(outputs, y) 와 squeeze()
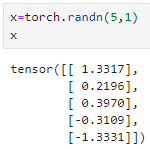
5행1열로 된 2차원 텐서를 만들었다.
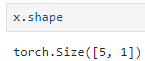
size=[5,1] 첫번째 차원이5, 두번째 차원이1
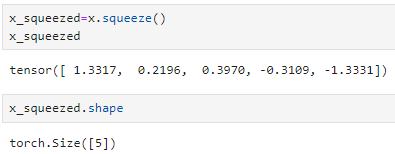
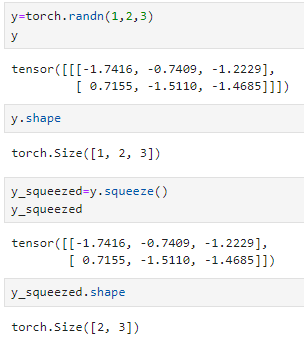
squeeze()의 다른 예시

그렇다면 squeeze(-1)은 무슨 뜻일까?
의문점output=[배치크기,1], y=[배치크기]로 올수도 있으니까 ( outputs squeeze(-1) , y.squeeze(-1)) 로 써야 더 맞을것 같다.
loss.backward()optimizer.step()
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')
10에포크마다 손실값을 출력하는 부분
ANN에서 다룬것과 거의 비슷하다.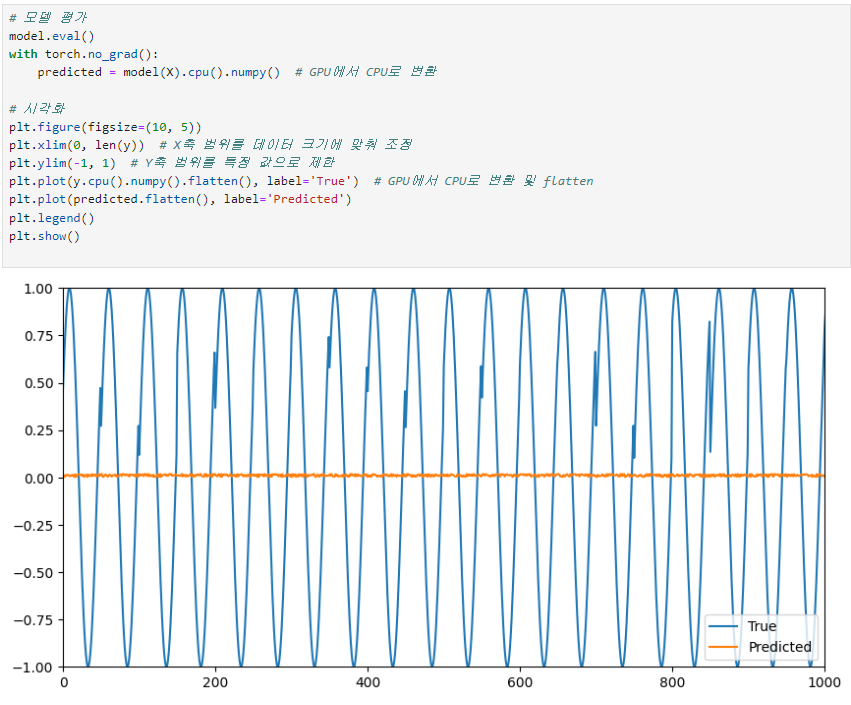
평가하는 부분에서 볼 것은 결과그래프이다.
True(원래값)는 사인함수처럼 잘 나오고 있는데, predicted를 보면 거의 0 근처에서 움직이고 있다.
이는 예측을 잘 하지 못하고 있음을 의미한다. 실제로 학습에서도 100에포크 후 loss가 0.4967 이었다.
LSTM과 GRU를 사용하면 이러한 문제가 해결될 수 있을지 다음번에 알아보도록 하겠다.