이번에는 RNN모델이 아닌 LSTM을 이용해 사인파동 예측모델을 다시 동작시켜 볼 것이다.
RNN의 단점은 장기 의존성 문제로, 시간이 지나면서 정보가 소실되거나 변형되는 것이다.
이를 해결하기 위해 LSTM은 ;셀 상태'와 세 가지의 '게이트'를 도입했다.
셀 상태는 일종의 기억저장소이다.
셀에 기억을 업데이트하거나 저장, 삭제하기 위해 입력게이트, 출력게이트, 망각게이트가 필요하다.
입력게이트는 어느 정도의 새로운 정보를 업데이트할지 결정하고,
망각게이트는 셀 상태에서 어떤 정보를 잊을지 결정한다.
입력게이트와 망각게이트가 작동해서 셀을 업데이트하면, 출력게이트에서 셀의 어느부분을 출력할지 결정한다.
출력한 결과는 최종적으로 은닉상태에 전달되어 다음 타임스텝에서 입력값으로 전달되거나, 최종 출력값으로 나오기도 한다.
전체 코드
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
def create_sine_wave_data(seq_length, num_samples):
X = []
y = []
for _ in range(num_samples):
start = np.random.rand()
x = np.linspace(start, start + 2 * np.pi, seq_length)
X.append(np.sin(x))
y.append(np.sin(x[-1] + 0.1)) # 마지막 타임스텝에 대한 예측
return np.array(X), np.array(y)
seq_length = 50
num_samples = 1000
X, y = create_sine_wave_data(seq_length, num_samples)
# 데이터셋을 PyTorch 텐서로 변환
X = torch.tensor(X, dtype=torch.float32).unsqueeze(-1) # [1000, 50, 1]
y = torch.tensor(y, dtype=torch.float32).unsqueeze(-1) # [1000, 1]
# 하이퍼파라미터 설정
input_size = 1
hidden_size = 64
output_size = 1
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class SimpleLSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleLSTM, self).__init__()
self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
h0 = torch.zeros(1, x.size(0), hidden_size).to(x.device) # 초기 은닉 상태
c0 = torch.zeros(1, x.size(0), hidden_size).to(x.device) # 초기 셀 상태
out, _ = self.lstm(x, (h0, c0))
out = self.fc(out[:, -1, :]) # 마지막 시간 단계의 출력
return out
# 모델 정의 및 GPU로 이동
model = SimpleLSTM(input_size, hidden_size, output_size).to(device)
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 데이터를 GPU로 이동
X, y = X.to(device), y.to(device)
# 모델 학습
num_epochs = 100
for epoch in range(num_epochs):
model.train()
outputs = model(X)
optimizer.zero_grad()
loss = criterion(outputs, y)
loss.backward()
optimizer.step()
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')
print('Finished Training')
# 모델 평가
model.eval()
with torch.no_grad():
predicted = model(X).detach().numpy()
# 시각화
plt.figure(figsize=(10, 5))
plt.plot(y.numpy().flatten(), label='True')
plt.plot(predicted.flatten(), label='Predicted')
plt.legend()
plt.show()
코드는 어제 했던것과 거의 비슷하다.
달라진 부분은

RNN은 초기 은닉상태(h0) 만 정하면 됐지만, LSTM은 초기 셀 상태(c0)를 설정하고
은닉상태와 셀상태 모두를 lstm에 전달해야 한다. self.lstm(x, (h0,c0))
당연히 출력물도 (out, (최종은닉상태, 최종셀상태)) 로 나온다.

학습결과물
이것만 봐도 어제 loss가 0.5에 가까웠던 것과 비교하여 학습이 아주 잘 되었음을 알 수 있다.

최종 그래프
잘 된 것 같기는 한데, 너무 겹쳐서 알아보기 힘들기 때문에 범위를 좀 제한해 보겠다.

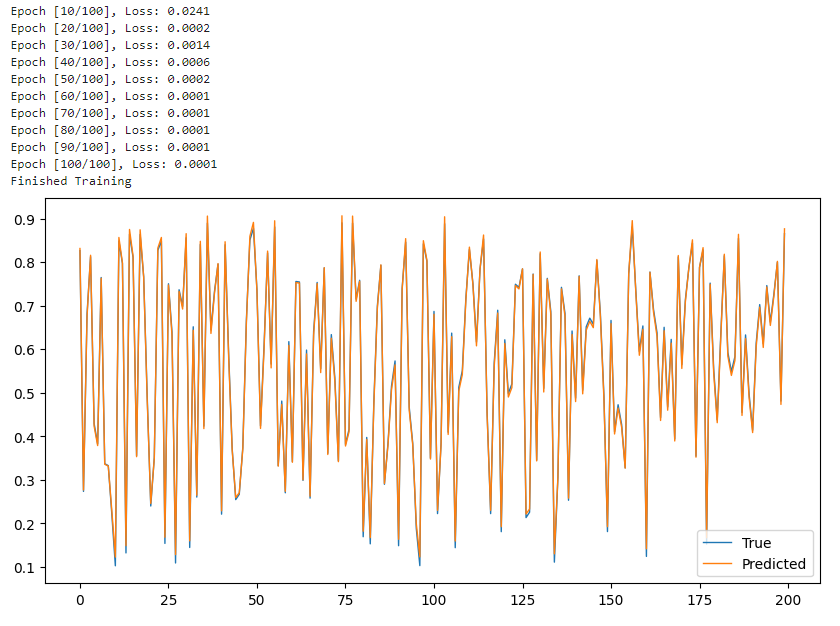
x축이 1000이었는데 뒷부분은 자르고 처음 200개의 데이터만 봤다. [:200]
True와 Predicted가 거의 일치하는 모습으로 보아 예측이 잘 되는 것 같다.
의문점: 사인그래프인데 왜 저렇게 뾰족뾰족하지.. 첨부터 잘못 그렸나..?
참고) GRU 모델로도 구현할 수 있을까?
GRU 모델 구현은 LSTM보다 더 쉽다. 셀 상태가 없기 때문에 사실상 RNN에서 RNN을 GRU로 바꾸기만 하면 되는 수준
GRU는 셀은 없고, 업데이트 게이트와 리셋게이트로 정보를 조절한다.

결과는 LSTM이랑 별 차이가 없다.